Jak obliczyć pole przekroju osiowego stożka?
W świecie geometrii i matematyki, stożki odgrywają istotną rolę dzięki swojemu unikalnemu kształtowi i właściwościom. W tym artykule przyjrzymy się, jak obliczyć pole przekroju osiowego stożka, co jest kluczowe nie tylko w teorii, ale i w praktycznych zastosowaniach inżynieryjnych i architektonicznych. Zrozumienie przekroju osiowego stożka oraz umiejętność obliczania jego pola stają się niezbędne dla studentów, inżynierów oraz pasjonatów matematyki.
Charakterystyka przekroju osiowego
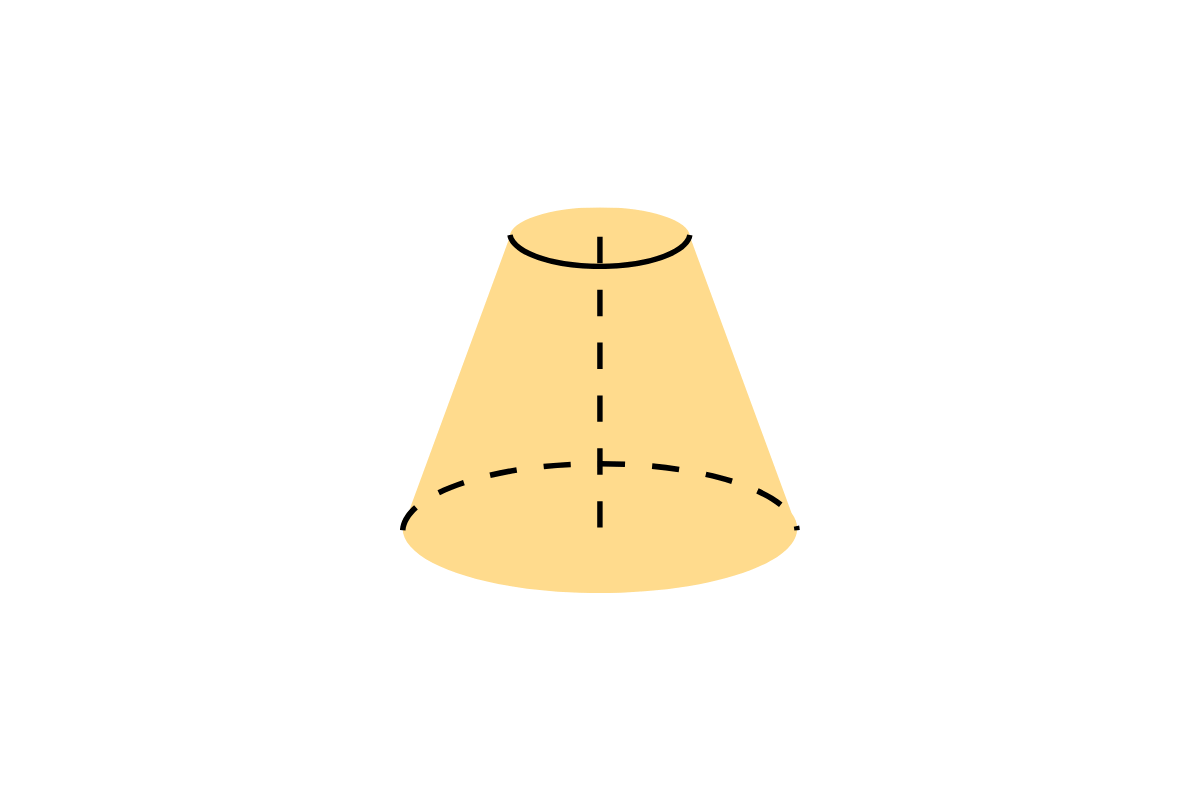
Przekrój osiowy stożka jest to figura powstała w wyniku przecięcia stożka płaszczyzną, która przechodzi przez jego oś symetrii. Taki przekrój, w zależności od kąta, pod jakim jest wykonany, może przybierać różne kształty. Najczęściej spotykanym przypadkiem jest przekrój osiowy o kształcie trójkąta równoramiennego, którego wierzchołek znajduje się w wierzchołku stożka, a podstawa jest równoległa do podstawy stożka.
Geometria przekroju osiowego
Przekrój osiowy stożka najczęściej ma kształt trójkąta równoramiennego. Wysokość tego trójkąta odpowiada wysokości stożka, natomiast podstawa trójkąta odpowiada długości podstawy stożka. Warto zaznaczyć, że kąty w przekroju osiowym mogą się zmieniać w zależności od kąta rozwarcia stożka. Na przykład, dla kąta rozwarcia wynoszącego 45 stopni, przekrój będzie miał specyficzny kształt, w którym wysokość i długość podstawy są równe.
Metoda obliczania pola
Aby obliczyć pole przekroju osiowego stożka, musimy skorzystać z odpowiedniego wzoru. Pole przekroju osiowego stożka wynosi w zasadzie pole trójkąta, które można obliczyć według wzoru: P = 1/2 * b * h, gdzie b to długość podstawy, a h to wysokość. W przypadku stożka, długość podstawy jest równą średnicą podstawy stożka, a wysokość odpowiada wysokości stożka.
Niezbędne dane do obliczeń
Aby wykonać obliczenia dotyczące pola przekroju osiowego stożka, potrzebujemy kilku danych. Przede wszystkim musimy znać wysokość stożka (h) oraz długość promienia podstawy (r). Znając te wartości, możemy łatwo obliczyć długość podstawy przekroju osiowego. W przypadku stożków równoramiennych, kąt rozwarcia stożka również ma istotne znaczenie, ponieważ wpływa na kształt i wielkość przekroju.
Przykład obliczeniowy
Rozważmy prosty przykład obliczenia pola przekroju osiowego stożka. Załóżmy, że mamy stożek o wysokości 10 cm i promieniu podstawy 5 cm. Aby obliczyć pole przekroju osiowego, najpierw obliczamy długość podstawy, co daje nam 2 * r = 10 cm. Następnie stosujemy wzór na pole trójkąta: P = 1/2 * b * h = 1/2 * 10 cm * 10 cm = 50 cm². W ten sposób otrzymujemy pole przekroju osiowego stożka wynoszące 50 cm².
Wpływ parametrów na pole przekroju
Pole przekroju osiowego stożka zmienia się w zależności od jego wymiarów. W miarę zwiększania wysokości stożka, pole przekroju osiowego również będzie rosło, przy założeniu, że promień podstawy pozostaje stały. Kąt rozwarcia stożka również ma istotny wpływ na pole przekroju osiowego – im większy kąt rozwarcia, tym bardziej „rozciągnięty” jest kształt przekroju osiowego, co prowadzi do zmiany długości podstawy i wysokości trójkąta.
Praktyczne zastosowania
Obliczenia pola przekroju osiowego stożka mają ogromne znaczenie w inżynierii oraz architekturze, gdzie precyzyjne obliczenia są kluczowe dla bezpieczeństwa i funkcjonalności budynków. W przemyśle budowlanym, pole to jest wykorzystywane do projektowania silosów i zbiorników na materiały sypkie. W obliczeniach dotyczących statków powietrznych, pole przekroju osiowego stożka ma kluczowe znaczenie dla aerodynamiki, ponieważ wpływa na opór powietrza i stabilność.
Zastosowanie w naukach przyrodniczych
W naukach przyrodniczych, pole przekroju osiowego stożka może być wykorzystywane do analizy różnych zjawisk i struktur naturalnych. Na przykład, geolodzy mogą badać stożki wulkaniczne, aby zrozumieć, jak ich kształt wpływa na erupcje i przepływy lawy. Również w biologii, zrozumienie kształtów brył może pomóc w badaniach nad rozwojem organizmów i ich adaptacją do różnych warunków środowiskowych.