Promień a średnica: wyjaśniamy różnicę, podajemy wzory
W matematyce pojęcia takie jak promień i średnica odgrywają kluczową rolę w zrozumieniu elementów koła i okręgu. Choć te terminy są często używane zamiennie w codziennej mowie, w rzeczywistości mają one różne definicje i zastosowania. Zrozumienie różnicy między nimi jest istotne nie tylko dla uczniów, ale także dla każdego, kto chce lepiej pojąć tajniki geometrii. W tym artykule wyjaśnimy kluczowe różnice między promieniem a średnicą, oraz ich znaczenie w kontekście koła i okręgu.
Promień i średnica – kluczowe różnice
Promień i średnica są fundamentalnymi pojęciami w geometrii, które pomagają opisać właściwości okręgu i koła. Te pojęcia można zdefiniować następująco:
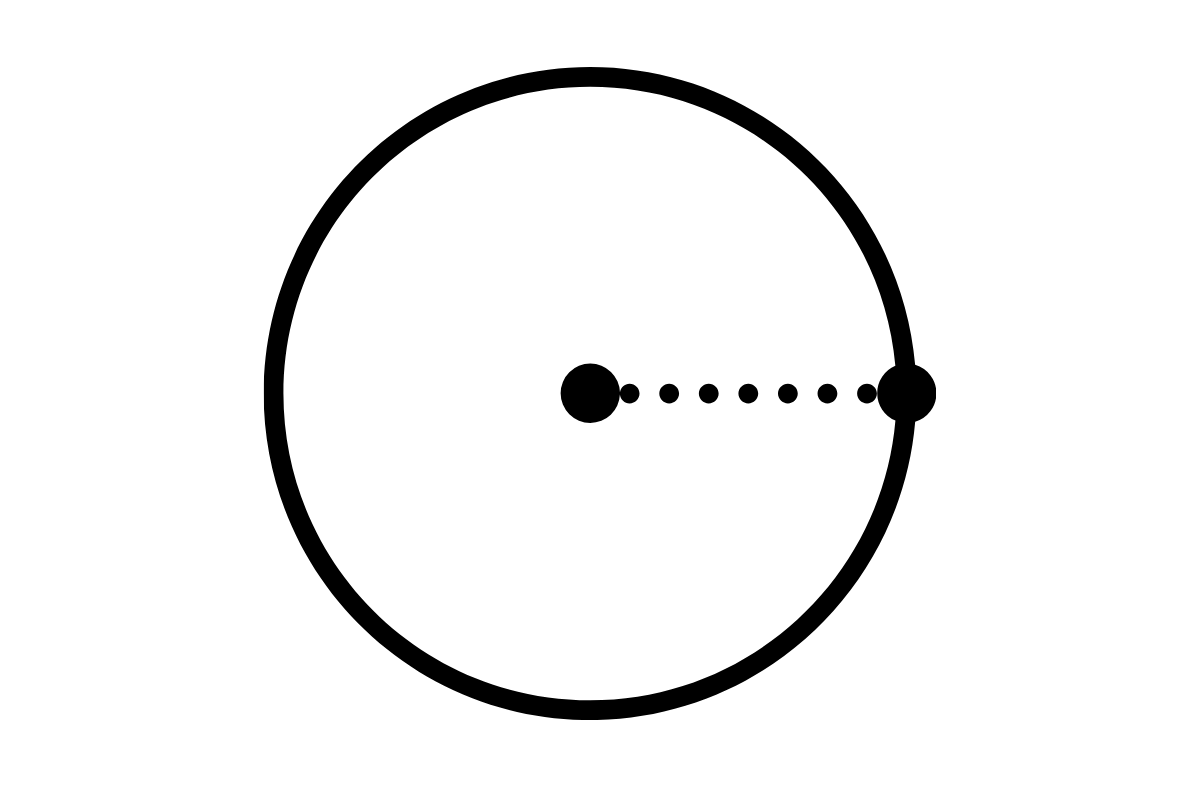
- Promień odnosi się do odcinka łączącego środek okręgu z dowolnym punktem na jego obwodzie.
- Średnica to odcinek przechodzący przez środek koła, łączący dwa przeciwległe punkty na obwodzie.
Średnica jest najdłuższą cięciwą okręgu i zawsze jest dwa razy dłuższa od promienia. Te różnice są kluczowe dla zrozumienia geometrii i pozwalają na precyzyjne obliczenia związane z polem koła, obwodem koła oraz innymi elementami geometrycznymi.
Definicja promienia okręgu
Promień okręgu, nazywany również długością promienia, to odcinek, który łączy środek okręgu z dowolnym punktem na jego obwodzie. Jest to podstawowy element w geometrii, pozwalający na dokładne określenie wielu innych właściwości koła i okręgu. Promień symbolizowany jest często literą 'r’. Odległość od środka koła do dowolnego punktu na obwodzie jest stała, co czyni promień kluczowym elementem w obliczeniach matematycznych, takich jak pole koła czy obwód koła. Jego definicja jest prosta, a jednocześnie niezwykle ważna w kontekście zrozumienia innych pojęć geometrycznych.
Definicja średnicy
Średnica okręgu to odcinek przechodzący przez środek koła i łączący dwa przeciwległe punkty na jego obwodzie. Jest ona najdłuższą cięciwą okręgu i jest równa dwukrotności promienia. Średnica symbolizowana jest często literą 'd’ i jest kluczowym elementem w wielu wzorach matematycznych, takich jak obliczenia obwodu koła czy pola koła. Średnica jest prostym, ale niezwykle ważnym pojęciem w geometrii, które pomaga zrozumieć strukturę i właściwości okręgów i kół.
Związek między promieniem a średnicą
Związek między promieniem a średnicą jest prosty, ale fundamentalny: średnica jest zawsze dwa razy dłuższa od promienia. Oznacza to, że jeśli znamy długość promienia, możemy łatwo obliczyć długość średnicy, mnożąc ją przez dwa. Ten związek jest kluczowy w wielu obliczeniach matematycznych związanych z geometrią kół i okręgów, takich jak obliczanie obwodu koła czy jego pola. Zrozumienie tego związku pozwala na lepsze zrozumienie struktury i właściwości geometrycznych kół i okręgów, oraz ich zastosowanie w praktyce.
Obliczanie długości promienia i średnicy
Obliczanie długości promienia i średnicy to podstawowe zadanie w geometrii, które wymaga zrozumienia relacji między tymi dwoma elementami koła i okręgu. Aby obliczyć długość promienia, musimy znać jedną z podstawowych właściwości okręgu, takich jak jego obwód lub pole koła. Oto jak to zrobić:
- Jeśli znamy obwód koła, możemy obliczyć długość promienia, dzieląc obwód przez 2 razy π (pi). Wzór na obwód koła to 2πr, gdzie 'r’ oznacza promień.
- W przypadku pola koła, korzystamy ze wzoru πr², co pozwala nam na obliczenie promienia, gdy znamy powierzchnię koła.
Podobnie, aby obliczyć średnicę, można skorzystać z prostego wzoru: średnica jest dwa razy dłuższa od promienia, co oznacza, że jeśli znamy długość promienia, wystarczy pomnożyć ją przez 2, aby uzyskać długość średnicy. Znajomość tych wzorów i umiejętność ich zastosowania jest kluczowa w matematyce, szczególnie w kontekście geometrii, gdzie precyzyjne obliczenia są niezbędne do rozwiązywania problemów. Niezależnie od tego, czy pracujemy z okręgiem o środku w punkcie (x, y) na płaszczyźnie, czy z bardziej skomplikowanymi kształtami geometrycznymi, umiejętność obliczania promienia i średnicy jest fundamentalna dla zrozumienia struktury i właściwości tych figur.
Przykłady zastosowania wzorów
Przykład obliczeń dla promienia i średnicy
Rozważmy okrąg o środku w punkcie (0,0) i promieniu o długości 5 jednostek. Znając promień, możemy łatwo obliczyć średnicę, korzystając z faktu, że średnica jest dwa razy dłuższa od promienia. W tym przypadku średnica wynosi 10 jednostek. Te obliczenia są kluczowe w matematyce, ponieważ pozwalają na dokładne określenie innych elementów koła i okręgu. W praktyce obliczenia promienia i średnicy są niezbędne w wielu dziedzinach, takich jak inżynieria czy architektura, gdzie precyzyjne wymiary są kluczowe.
Przykład obliczeń obwodu i pola koła
Korzystając z wcześniej ustalonego promienia naszego okręgu, możemy obliczyć obwód koła za pomocą wzoru 2πr. Dla promienia równym 5 jednostkom, obwód wynosi 10π jednostek. Podobnie, pole koła można obliczyć używając wzoru πr², co daje 25π jednostek kwadratowych. Te wzory są fundamentem w geometrii i są używane do wielu praktycznych zastosowań, takich jak:
- projektowanie kół zębatych
- obliczanie powierzchni działek
Znajomość tych obliczeń jest nieodzowna dla każdego, kto zajmuje się naukami ścisłymi.
Przykłady w praktyce matematycznej
W praktyce matematycznej, wzory dotyczące promienia, średnicy, obwodu i pola koła znajdują szerokie zastosowanie. Na przykład, w geometrii analitycznej, okrąg o środku w punkcie (h, k) i promieniu r jest opisany równaniem (x-h)² + (y-k)² = r². Takie równania pozwalają na analizę właściwości okręgów w kontekście płaszczyzny współrzędnych. W praktyce, umiejętność szybkiego obliczania długości promienia czy pola koła jest przydatna nie tylko w teorii, ale także w rozwiązywaniu codziennych problemów matematycznych, takich jak obliczenia związane z projektowaniem przestrzeni.